从划分数到杨表

Posted on | In

从划分数到杨表

Chapter 0 发现问题

你是一个普通的高中生.一天,你在做你的数学作业,或者看科普书籍时发现了这样一个问题:

求任意正整数\(n\)的无重复分划个数\(p(n)\).无顺序.可重复.

形式化的,\(p(n)=card(S),S=\{a|a\in \mathbb N^+,\sum \limits _{i \in a}i=n\}\)

现在可以停下来找找规律,祝你成功.

然后,你用接下来的一整天,在伟大的互联网和你的VSCode的帮助下,学会了很多有关的知识.很可惜,并不包括\(p(n)\)的通项公式.

Chapter 1 枚举

你当然要先枚举一下找找规律.你轻而易举的发现了\(p(1)=1,p(2)=1,p(3)=2,p(4)=2,p(5)=3,p(6)=4\).但是你并没有发现什么规律.

Chapter 2 dp

正当你思考要不要把枚举扩展到\(10\)的时候,你突然想起自己有一个光荣的身份:(可能是前)信息竞赛生!

于是你打开你的VSCode或者是Dev-C++,开始思索它的dp解法.

很明显,这个问题看起来像是背包问题求可能总数,还是01背包.你立刻有了一个\(O(n^2)\)的算法.

int p[maxn];

int solve(int n){
	p[0]=1;
	for(int i = 1; i <= n; i++){//i表示j的分划中最大数为i
        for(int j = (i*(i+1)/2); j >= i; j--){//不可重复。枚举顺序参考01背包。
            if(j >= maxn) continue;
            p[j]+=p[j-i];
        }
    }
    return p[n];
}

你发现这份代码的结果和你写的前几项是吻合的,于是你认为它是对的.

但是这还没完.

Chapter 3 扩展

在胜利的鼓舞下,你开始思考一个新问题:如果划分可以重复又怎么样呢?

很快地,你修改好了你的代码

int q[maxn];

int solve(int n){
	q[0]=1;
	for(int i = 1; i <= n; i++){//i表示j的分划中最大数为i
        for(int j = i; j <= n; j++){//可重复。枚举顺序参考完全背包。
            if(j >= maxn) continue;
            q[j] += q[j-i];
        }
    }
    return q[n];
}

Chapter 4 生成函数

WARNING:这章有较多的公式，如果对自己的耐性没有信心建议直接阅读Chapter5

怎么说呢……\(O(n^2)\)的算法还是有点慢啊。有没有更快一点的方法呢？比如\(O(n\log n)\)?\(O(n)\)?或者……甚至\(O(1)\)?

如果要更快的做法就只能上点数学了吧……

你想起了组合数学常用套路——生成函数！

设\(f(x)=\sum\limits_{i=0}^\infty p(i)x^i\)，\(f(x)\)的第\(n+1\)项自然也可以表示成在每个\((1+x^i)\)项中取一个组成\(x^n\)的方法数。

也就是说，\(\sum\limits_{i=0}^\infty p(i)x^i=\prod\limits_{i=0}^\infty (1+x^i)\).第\(1\)项显然是\(1\),就不管了。

well……到这一步你也不会解了。那就看看\(q(x)\)吧。

设\(g(x)=\sum\limits_{i=0}^\infty q(i)x^i, g(x)\)亦等于\(\prod \limits_{i=0}^\infty (\sum\limits_{j=0}^\infty x^{ij})=\prod \limits_{i=0}^\infty (x^i\sum\limits_{j=1}^\infty x^j)\),设\(x \in (0,1)\)\(g(x)=\prod \limits _{i=0}^\infty (\frac{1}{1-x^i})\)

看起来好像没什么关系……吗？

把\(f(x)\)改成和\(g(x)\)一样的形式试试。

\(\prod\limits_{i=0}^\infty (1+x^i)=\prod\limits_{i=0}^\infty \frac{1-x^{2i}}{1-x^i}\)有点像了。但是上面多了一项。能不能消去呢？

\(\prod\limits_{i=0}^\infty \frac{1-x^{2i}}{1-x^i}=\frac{\prod \limits _{i=0}^\infty (1-x^{2i})}{\prod \limits _{i=0} ^{\infty}(1-x^i)}\)上面只有偶数项，下面有所有正整数项。所以消去上面的项也就有\(f(x)=\prod \limits_{i=0}^\infty \frac{1}{(1-x^{2i+1})}\)

和\(g(x)\)一对比……这不就是说只有奇数的可重划分吗！

但是这是为什么呢？

换句话说，有没有奇数可重复划分和正整数不可重复划分的一一对应呢？

Chapter 5 Young图

其实我一直没很明白Ferrer图和Young图的区别。但是我先学的是Young表，所以我就叫它Young图了。

你想起了这样一句名言：“如果你发现自己找不到某些东西的规律，想想这是不是什么高维事物的投影”。你忘记这是谁说的了，好像是一个日本青春校园小说的女主角之一。但是反正你觉得她说的很有道理。

如果要将\(7=1+2+4\)变成什么二维的东西，最容易想到的方法自然是这样.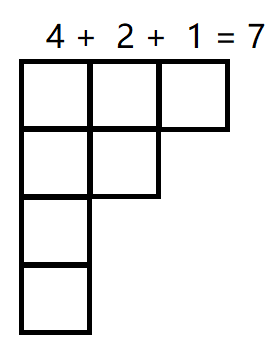Young_Diagram.png

此时你也许会突然发现这和你教练讲过的一种叫Young表的数据结构很像。如果你在网上搜了搜，会发现它叫Young图。也叫Ferrers图。

则，奇数划分就是这样.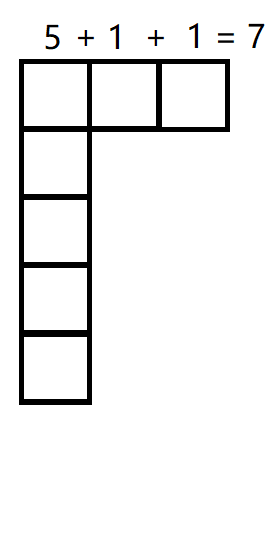Young_Diagram_odd.png

如果要在奇数划分和正整数划分间作一一对应，就要寻找其特点废话。很容易发现的方法就是将奇数划分的图分成一个个相邻的矩形。Young_Diagram_odd_couloured.png

但是你如果实践几个数，将会很快发现问题：\(5\times1\)和\(1\times5\)是相同的.更抽象的说，你无法区分带有多个奇数因子或者没有偶数因子的矩形.这是在奇数到正整数的问题.从正整数到奇数的对应中,你也无法区分\(5\)和\(1+4\).第二种分划会被写成一个宽\(5\)高\(1\)的矩形,而第一种会被写成...

等等,这两种情况是一一对应的!只需要对矩形进行分割!

反过来想,从正整数到奇数的对应,如果两个数对应的矩形是一样高的,说明对应的偶数或者\(1\)是相同的.换句话说,两个数的\(lowbit\)相同.那就可以对每个矩形的"宽"进行二进制的分组.

形式化地,对每个宽\(m\)高\(n\)的矩形,计\(P(m)=\{x=2^n|m\&x==x,n \in \mathbb N^+\}\),则\(R(m,n)=\{(x,n)|x \in P(m)\}\)即为该矩形分划成的矩形的集合,其中每个元素\((x,y)\)代表宽为\(x\),高为\(y\)的矩形.

容易证明任何奇数划分可以用这种方法变成正整数的限制划分.

至于正整数限制划分变成奇数划分,就是将其分解为奇数和偶数或1的乘积啦...容易发现这是唯一的.

形式化地,对每个正整数的分划\(a\)(\(a\)的定义参考Chapter0),\(R(a)=\{(x,y)|x=\sum \limits_{i\in a 且lowbit(i)=y}\frac i {lowbit(i)}\}\).

Chapter 6 (不知道什么时候才会写的)五边形数定理

WARNING:该章节并没有完成.

但是你忽然发现自己还是没有降低时间复杂度啊...